မြန်မာနဲ့သင်္ချာ

Dear curious non-Burmese visitors, this page is obviously intended for the Burmese audience. Most of the available Burmese books and articles in mathematics beyond high school are often just a collage of facts and terminologies cramped in a popular science style with no pinch of logical rigour whatsoever. This, together with the language barrier usually hides mathematical elegance from young aspiring students. This page contains several results and ideas in mathematics that fascinated me during my first steps, written in an informal way without losing (much) rigour. You are welcome to flip around the pages and browse through some pictures.

သင်္ချာရဲ့အလှက “ဘာလို့မှန်သလဲ” ဆိုတဲ့အကြောင်းပြချက်တွေရဲ့ကွန်ယက်နဲ့ ဆက်စပ်နေလေ့ရှိပါတယ်။ ဒီပေ့ချ်မှာတင်ထားတဲ့စာစုလေးတွေက ကျွန်တော်သင်္ချာကို စလေ့လာတုန်းက အတော်လေးကြိုက်ခဲ့မိတဲ့မှန်ကန်ချက်တချို့နဲ့ သူတို့ရဲ့နောက်ကွယ်က ပိုပြီးနက်ရှိုင်းတဲ့သင်္ချာတွေကို mathematical rigour အတတ်နိုင်ဆုံး မပျက်စီးစေဘဲ မြန်မာလိုရေးထားတာပါ။ ကျွန်တော်စာသင်တဲ့အခါ ကျောင်းသားတွေကိုပြလေ့ရှိတဲ့သင်္ချာမျက်လှည့်တွေ၊ ပြောလေ့ရှိတဲ့ဉာဏ်စမ်းတွေကိုလည်း တင်ပေးထားပါတယ်။ ဒီစာစုတွေသည် အထက်တန်းကျောင်းသားကျောင်းသူတွေနဲ့ သူတို့ကိုစာသင်ကြားပေးနေတဲ့ ဆရာဆရာမတွေအတွက် အဓိကရည်ရွယ်ထားတာဖြစ်ပါတယ်။

ပဟေဠိများ

• ဦးထုပ်နီ ဦးထုပ်ပြာ pdf
  ထောင်တစ်ခုမှာ ထောင်သားအယောက် 100 ရှိပါတယ်။ တစ်နေ့မှာ ထောင်မှူးဟာ ထောင်သားတစ်ယောက်စီ ကိုခေါ်ပြီး ဦးထုပ်အနီ (သို့မဟုတ်) အပြာတွေကိုဆောင်းပေးပါတယ်။ ဆောင်းပေးအပြီးမှာ ထောင်သားအားလုံးကို “မင်းတို့ ခေါင်းပေါ်မှာ ဦးထုပ်အနီ (သို့မဟုတ်) အပြာရှိတယ်။ အနီရောင်ဆောင်းထားတာ အနည်းဆုံးတစ်ယောက်ပါတယ်၊” လို့ကြေညာလိုက်ပါတယ်။ အမှန်မှာတော့ ဦးထုပ်အနီကအလုံး 40 နဲ့ ဦးထုပ်အပြာက အလုံး 60 ရှိတာပါ (ဒါကိုတော့ ထောင်သားတွေ မသိပါဘူး)။ ထောင်သားတိုင်းဟာ မိမိခေါင်းပေါ်ကဦးထုပ်ရဲ့အရောင်ကို ဘယ်နည်းနဲ့မှမြင်ဖို့ မဖြစ်နိုင်အောင် လုပ်ထားပါတယ်။ ဒါပေမယ့် တခြားထောင်သားတွေ အားလုံးရဲ့ ခေါင်းပေါ်က ဦးထုပ်အရောင်တွေကိုတော့ မြင်နေရပါတယ်။ ထောင်သားအချင်းချင်း ဘယ်နည်းနဲ့မှ အဆက်အသွယ် လုပ်လို့မရပါဘူး။ နေ့တစ်နေ့ရဲ့ နံနက်ခင်းတိုင်းမှာ ထောင်သားတစ်ယောက်ချင်းစီကို သီးသန့်လာတွေ့ပြီး “မင်းခေါင်းပေါ်က ဦးထုပ်ဟာ ဘာအရောင်လဲမင်းသိပြီလား၊ သိပြီဆိုရင် မင်းမှန်ကြောင်းသက်သေပြ” လို့လိုက်မေးပါတယ်။ သက်သေပြချက် လုံးဝဥဿုံခိုင်လုံတဲ့ ထောင်သားတွေကို အဲ့ဒီနေ့ရဲ့နေ့လယ်မှာ ထောင်သားအားလုံးရဲ့ရှေ့မှောက်တင်ပဲ ပေါ်ပေါ်ထင်ထင် လွှတ်ပေးမယ်လို့လည်း ကြေညာထားပါတယ်။ တစ်ခုရှိတာသည် ထောင်သားတွေဟာ အင်မတန်မှကို ဉာဏ်ကောင်းလှပါတယ်။ ဆိုလိုတာက လွတ်ဖို့ နည်းလမ်းရှိရင် ရအောင်ကိုလွတ်နိုင်တဲ့သူတွေပါ။ ဒီလိုဉာဏ်ကောင်းတာကို ထောင်သားအချင်းချင်းရော၊ ထောင်မှူးကပါ သိပါတယ်။
  မေးခွန်း။ ။ ဦးထုပ်များဆောင်းပေးအပြီး 42 ရက်မြောက်နေ့မရောက်ခင် ထောင်သားအားလုံးလွတ်မှာဖြစ်ကြောင်း သက်သေပြပါ။

• L ပုံတွေပိုင်းဖြတ်ခြင်း pdf
  $8\times 8$ ဘုတ်တစ်ခုထဲက တစ်ယူနစ်အကွက်လေးတစ်ကွက်ကို ဖြတ်ထုတ်လိုက်မယ်။ ဒါဆိုရင် ကျန်ခဲ့တဲ့အကွက် 63 ကွက်ပါဘုတ်ပြားကို L-ပုံစံအတုံးလေးတွေ (တစ်ယူနစ်အကွက် သုံးကွက်ကို L-ပုံစံဆက်ပြီး ရလာတဲ့အတုံး) နဲ့ အပြည့်ခင်းလို့ရကြောင်းပြပါ။ ဘယ်အကွက်ကိုဖြတ်ထုတ်လိုက်ထုတ်လိုက် အမြဲတမ်းခင်းလို့ရနေနိုင်မယ့်နည်းလမ်းကို တီထွင်ပြရမှာပါ။

• လမ်းလျောက်ထွက်ချဲလင့် pdf
  Jack ဆိုတဲ့လူတစ်ယောက်နေတဲ့ မြို့ကလေးဟာ မြစ်ဆုံမြစ်ခွတစ်ခုကို ဖြတ်လျက်တည်ထားပြီး မြစ်လယ်ကျွန်းတစ်ခု ပါဝင်ပါတယ်။ မြို့လေးရဲ့မြေပုံကိုတော့ ပုံမှာပေးထားပါတယ်။ မြို့ရဲ့ကုန်းမြေအစိတ်အပိုင်းတွေကို တံတားစုစုပေါင်း 7 စင်းနဲ့ချိတ်ဆက်ထားပါတယ်။ Jack ရဲ့နေအိမ်ကတော့ တံတားငါးစင်းဆုံရာ မြစ်လယ်ကျွန်းလေးပေါ်မှာပါ။ နံနက်ခင်းတစ်ခုမှာ Jack ဟာလမ်းထွက်လျောက်ဖို့ပြင်ဆင်နေရင်းနဲ့ ကိုယ့်ကိုယ်ကို ချဲလင့်လုပ်ဖို့ အိုင်ဒီယာတစ်ခု ရလိုက်ပါတယ်။ မြို့ရဲ့တံတားတွေအားလုံးကို အတိအကျတစ်ကြိမ်စီပဲ ဖြတ်ပြီးတော့ အဆုံးမှာသူ့အိမ်သူပြန်ရောက်အောင် မြို့ပတ်လမ်းလျောက်မယ့် challenge ပါ။ ဒါကြောင့် တံတားတိုင်းကိုဖြတ်ရမှာဖြစ်သလို တံတားတစ်ခုကိုတစ်ကြိမ်ထက် ပိုဖြတ်ခွင့်မရှိပါဘူး။ Jack က challenge ကိုမရမကအောင်နိုင်အောင်လုပ်နိုင်ခဲ့ပါတယ်။ ဒါပေမယ့် သူလူလည်ကျခဲ့ရတယ်။ တံတားတချို့ကိုနှစ်ကြိမ်မဖြတ်ချင်လို့ လှေစီးလိုက်တယ်တဲ့လေ။ ကဲ… စာဖတ်သူအနေနဲ့ Jack ရဲ့ challenge ကိုလှေမစီးဘဲ၊ မြို့ပြင်မထွက်ဘဲ အောင်မြင်အောင်လုပ်နိုင်သလား။ လှေစီးကိုစီးရမယ်ဆိုရင်ရော အနည်းဆုံးဘယ်နှကြိမ်စီးရမလဲ။
  

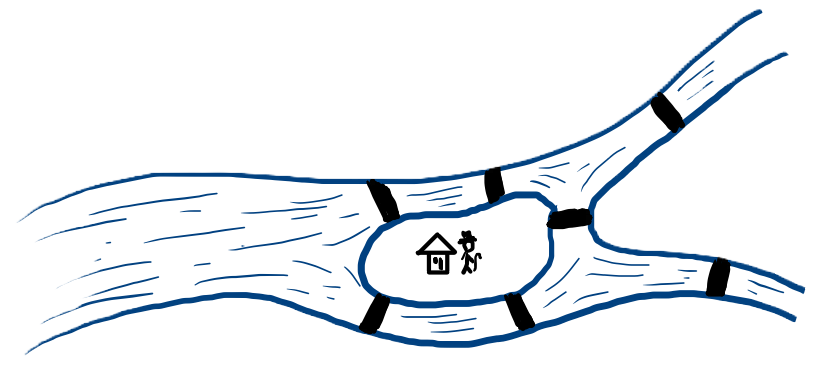
• ဒိုးဇက်အပြည့်ခင်းကြမယ် pdf
  $4\times 4$ grid တစ်ခုရဲ့ မျက်နှာချင်းဆိုင်ထောင့်စွန်နှစ်ခုက $1\times 1$ အကွက်နှစ်ကွက်ကို ပုံပါအတိုင်းဖြုတ်ယူလိုက်ပါ။ ရရှိလာတဲ့ ဘုတ်ပြားပေါ်မှာ $2\times 1$ အရွယ်ရှိတဲ့ ဒိုးဇက် (domino) 7 ခုကိုတင်လိုက်ပါမယ်။ ဖြစ်ချင်တာကတော့ ဘုတ်ပြားပေါ်မှာ နေရာလွတ်လုံးဝမကျန်တော့အောင် ကွက်တိတင်ချင်တာပါ။ တင်ဖို့ဖြစ်နိုင်သလား။ ဖြစ်နိုင်တယ်ဆိုရင်တင်ပြပါ။ မဖြစ်နိုင်ရင် မဖြစ်နိုင်ကြောင်း ရှင်းရှင်းလင်းလင်းတင်ပြပါ။
  

မျက်လှည့်နဲ့ဆော့စရာများ

• မင်းဘယ်မှာလဲငါသိတယ် pdf
  ဒါကတော့ ကျွန်တော်စာသင်ဖြစ်တဲ့ကျောင်းသားအားလုံးကို ပြဖြစ်အောင်ပြတဲ့မျက်လှည့်လေးပါ။ အခုစာဖတ်သူကိုလည်း စာအုပ်ထဲကနေပဲ မျက်လှည့်လှမ်းပြပါမယ်။ အောက်က $3\times 3$ grid ထဲက …

• တစ်လှမ်းလား နှစ်လှမ်းလား pdf
  ကျောက်ကမ်းပါးတစ်ခုရဲ့အစွန်းနားမှာ စက်ရုပ်လေးတစ်ရုပ်ရပ်နေပါတယ်။ စက်ရုပ်လေးက ရှေ့ကိုခြေလှမ်း ဆယ်လှမ်းပဲလှမ်းလို့ရပါတယ်။ အဲ့ထက်ပိုလှမ်းတာနဲ့ ချောက်ထဲပြုတ်ကျမှာပါ။ စာဖတ်သူနဲ့ ကျွန်တော်က ဒီစက်ရုပ်လေးကို တစ်လှည့်စီ ရှေ့တိုးဖို့ အမိန့်ပေးပါမယ်။ တိုးတဲ့အခါ တစ်လှမ်း သို့မဟုတ် နှစ်လှမ်း တိုးခိုင်းလို့ရပါတယ်။ ဒီထက်ပို လှမ်းခိုင်းလို့မရသလို နေရာမှာရပ်နေခွင့်လည်းမရှိပါဘူး။ စက်ရုပ်ကို ချောက်ထဲပြုတ်ကျအောင် မဖြစ်မနေ အမိန့်ပေးလိုက်ရတဲ့သူက အရှုံးဖြစ်ပါတယ်။ ကဲ… ကျွန်တော်နဲ့ဆော့ကြည့်ရအောင်။
  

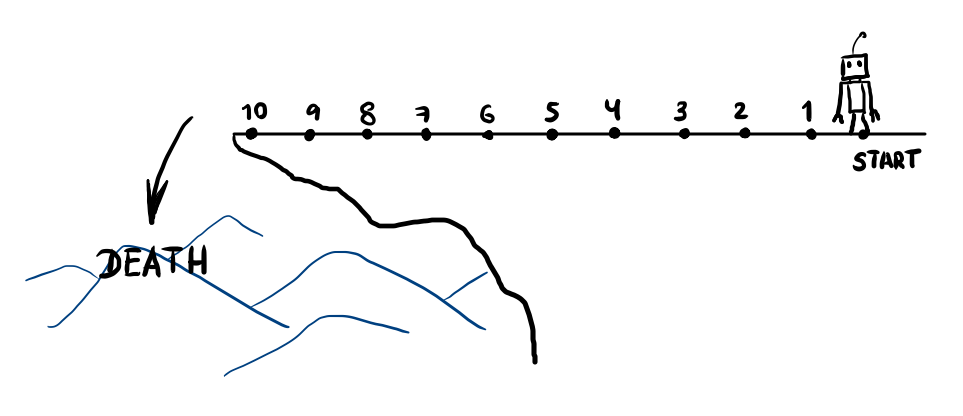
အထွေထွေသိမှတ်ဖွယ်ရာများ

• အနန္တထက်ပိုကြီးတဲ့ အနန္တ pdf
  သုညနဲ့တစ်ကြားက ကိန်းစစ်အရေအတွက်နဲ့ တစ်နဲ့သုံးကြားက ကိန်းစစ်အရေအတွက် ဘယ်ဟာပိုများသလဲ။ အနန္တထက်ပိုကြီးတဲ့ အရေအတွက်ဆိုတာရှိသလား။ အနန္တအစုတွေမှာ “ပိုများတယ်၊” “ပိုနည်းတယ်၊” ဆိုတဲ့စကားတွေက အဓိပ္ပါယ်ရှိသေးရဲ့လား။

• ထုပုံတွေရဲ့ အသက်ညီမျှခြင်း pdf
  ထုပုံတွေအားလုံးအတွက် ထိပ်စွန်းမှတ်အရေအတွက်၊ အနားစောင်းအရေအတွက်နဲ့ မျက်နှာပြင်အရေအတွက်တို့ကြားထဲမှာ ရှင်းလင်းတဲ့ဆက်သွယ်ချက်လေးတစ်ခုရှိပါတယ်။ ဒါဘာကြောင့်မှန်တာလဲ၊ ဒါသုံးပြီးတော့ အဘက်ဘက်ကခေါက်ချိုးညီတဲ့ထုပုံ ငါးခုပဲရှိကြောင်း ဘယ်လိုသက်သေပြကြမလဲ။

• သုညနဲ့ ဘာကြောင့်စားလို့မရတာလဲ pdf
  … ဒါဟာ ကိန်းဂဏန်းတွေနဲ့ ‘စားခြင်း’ ဆိုတဲ့ operation ကို လက်တွေ့လောကနဲ့နှိုင်းယှဉ်ပြီး စဉ်းစားကြည့်လို့ထွက်လာတဲ့ အဖြေပဲဖြစ်ပါတယ်။ ဒီလိုပဲ “မယုံရင်စားအိမ်နဲ့ချစားကြည့်လိုက်လေ” ဆိုတဲ့ သိပ်ကျေနပ်စရာမကောင်းတဲ့ အဖြေတွေလည်း တွေ့ရပါတယ်။ ဒါပေမယ့် ဒီဆောင်းပါးမှာတော့ သုညနဲ့ဘာလို့စားလို့မရတာလဲဆိုတဲ့ မေးခွန်းကို လက်တွေ့လောကနဲ့ လုံးဝမဆက်စပ်ဘဲ သင်္ချာရှုထောင့်စစ်စစ်ကနေ အဖြေပေးပါမယ်။ ပိုပြီးတိတိကျကျပြောရရင် algebra ရှုထောင့်ကနေ အဖြေပေးမှာပါ။ …

အိုလံပစ်သင်္ချာ

• Recursions in Combinatorics pdf
  သမားရိုးကျ အခြေခံ counting အိုင်ဒီယာတွေဖြစ်တဲ့ permutations and combinations သိပြီးသားကျောင်းသားကျောင်းသူတွေအတွက် တစ်ဆင့်ဆက်တက်လို့ရမယ့် topic တစ်ခုပါ။ “ပုစ္ဆာအကြီးကို ပုစ္ဆာအသေးလေးတွေဖြစ်အောင်ပြောင်းခြင်း” ဆိုတဲ့ အိုင်ဒီယာသည် combinatorics မှာမကြာခဏတွေ့နေရတဲ့ အိုင်ဒီယာပါ။ ဒီအိုင်ဒီယာကိုသုံးပြီး counting ပုစ္ဆာတွေကို ဘယ်လိုဖြေရှင်းကြမလဲ၊ counting မဟုတ်တဲ့ ပြဿနာတွေကိုရော ဘယ်လိုမျိုးအဖြေရှာလို့ရမလဲ စတာတွေအကြောင်းဖြစ်ပါတယ်။